GeoGebra CAS计算器是一款可以帮助用户计算函数的内容，可以将你的函数添加到软件分析，软件提供坐标系，可以直接将输入的函数显示在绘图区域，方便在坐标系求解函数，软件界面已经提供数学经常使用的函数内容，可以输入x、y、π、e、平方、多次方、开方、sin、tan、cos、log、In、10次方等多种求解内容，可以随意在软件输入表达式，可以自动求解结果，可以通过绘图的方式显示求解内容，无论是求解数学方程还是求导数和积分都可以在这款软件上执行。

软件功能

　　1、GeoGebra CAS计算器提供函数图像生成功能，可以通过分析函数图求解方程

　　2、在软件输入函数公式就可以自动在坐标系生成图像

　　3、可以注入就解方程，将方程公式输入到软件就可以在图像上展示方程内容，从而求解

　　4、支持展开代数式, 分解因式, 求导数和积分，提供的功能很多，轻松计算复杂的函数

　　5、CAS 格局包含 CAS 运算区和 绘图区. 默认情况下, 坐标轴显示在 绘图区. 根据激活的视图的不同, 绘图区工具栏或者 CAS 运算区工具栏显示在应用的顶部, 同时撤消/恢复按钮总是显示于右上角.

　　6、CAS 运算区允许您使用 GeoGebra 的 CAS (计算机代数系统) 进行符号计算f. 它由顶部的指令栏单元格和下方的输出显示单元格组成. 您可以与普通代数区指令栏相同的方式使用此指令栏

　　7、GeoGebra 工具栏提供了一系列 CAS 运算区专用的工具. 您可以通过单击显示相应图标的按钮来激活工具.

　　8、使用精确解工具和因式分解工具, 解方程和分解因式.

　　9、您可以将 CAS 运算区的功能与 绘图区的绘图功能结合在一起.

　　注意: 取决于哪个视图处于激活状态, 哪个视图(绘图区或者 CAS 运算区) 的工具栏就显示在应用的顶部.

软件特色

　　1、GeoGebra CAS计算器提供丰富的函数计算功能

　　2、可以在软件直接运算函数，可以在软件直接添加函数

　　3、直接输入公式就可以在软件选择精准结果，这样就可以显示求解内容

　　4、可以在软件选择因式分解，可以在软件选择积分求解

　　5、每个输入的内容都可以在软件显示求解内容，也可以在绘图界面显示函数图

　　6、支持解方程, 展开代数式, 分解因式, 求导数和积分

　　7、支持表格功能，可以直接通过表格录入数据求解

　　8、支持颜色设置，可以在软件定义函数图的颜色效果，方便标注函数

使用说明

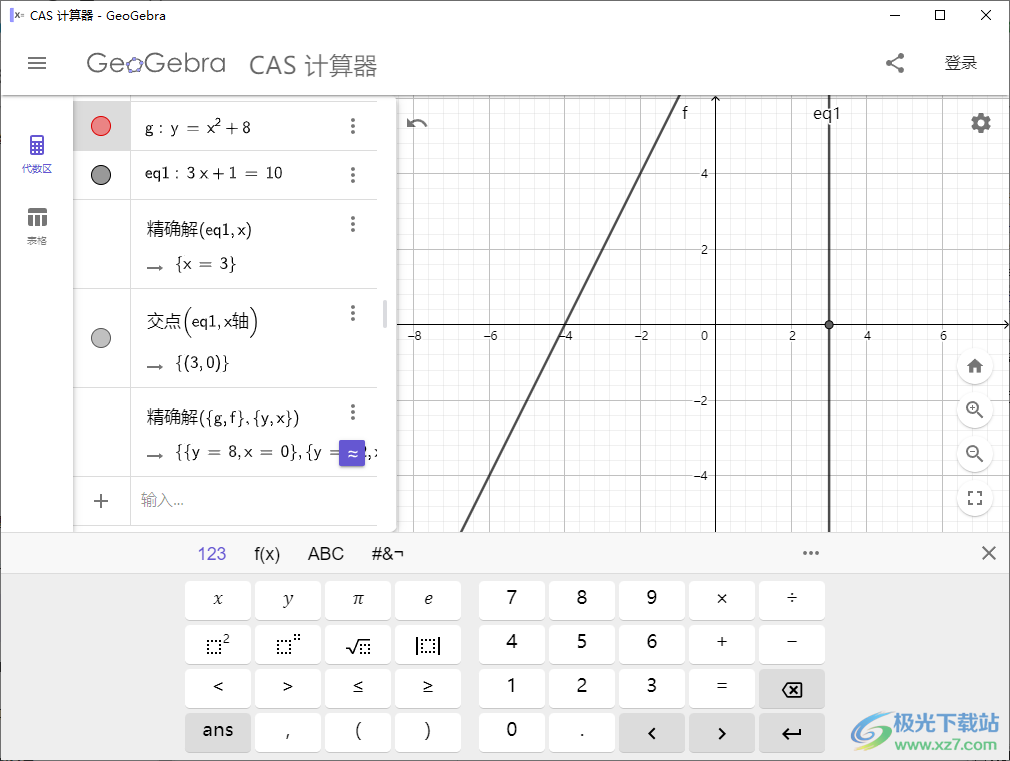
　　1、将GeoGebra CAS计算器打开就可以在软件界面输入函数内容

　　2、可以在软件直接计算各种函数，输入数值就可以显示结果，也可以在绘图界面显示图形

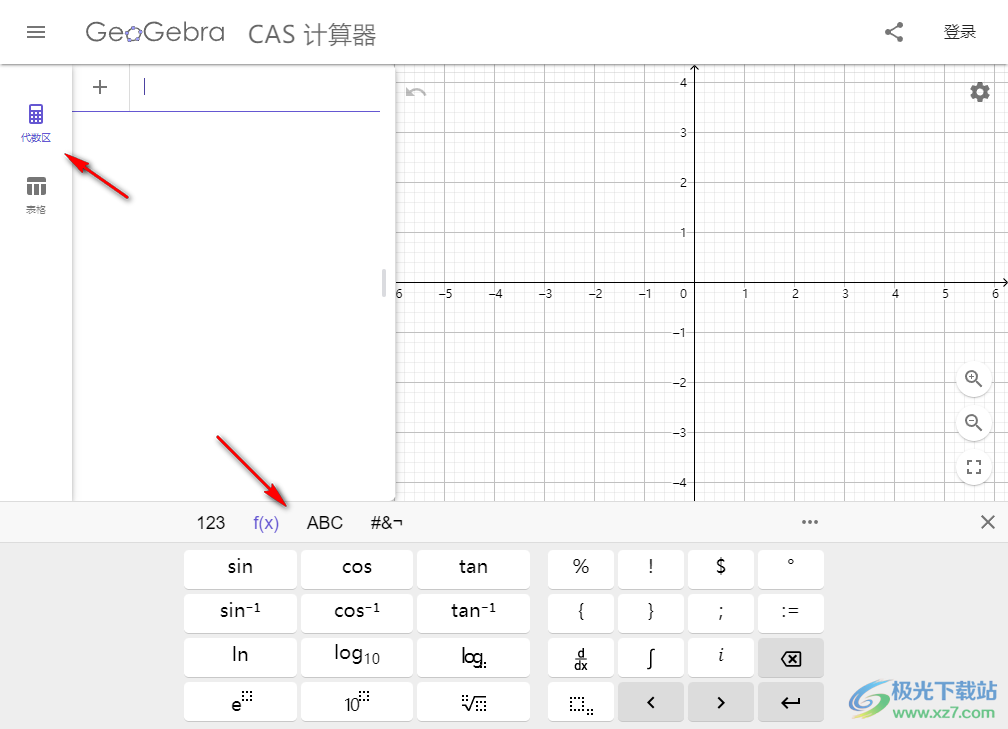
　　3、底部是输入区域，提供很多函数公式，数值直接通过键盘输入就可以了

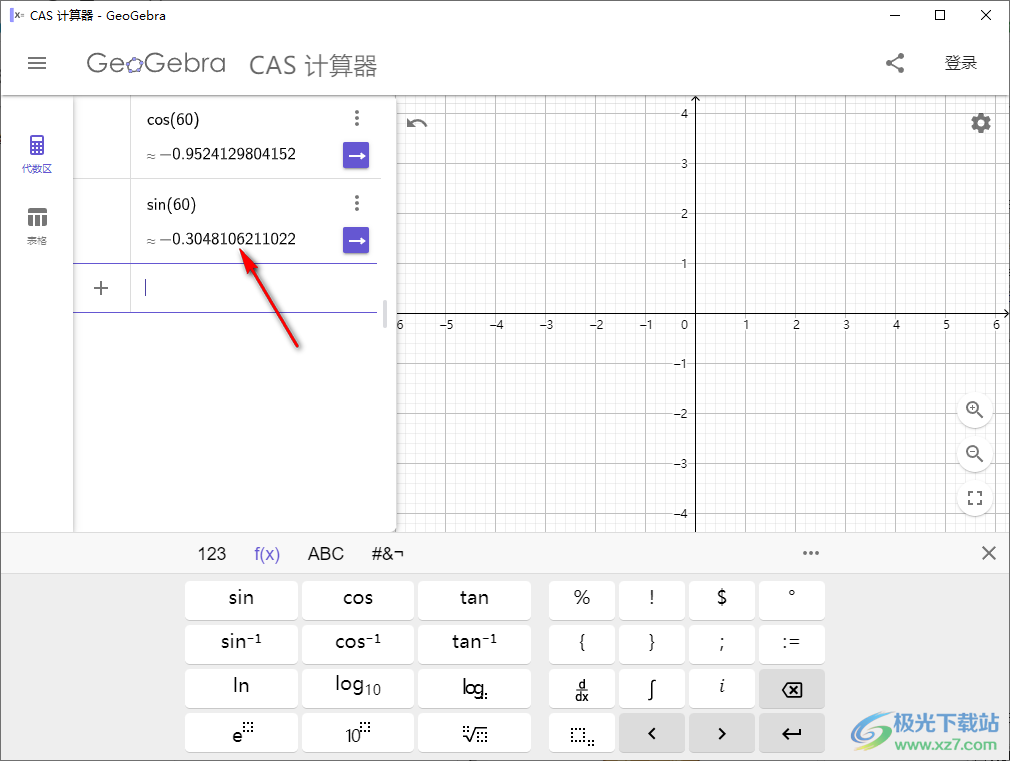
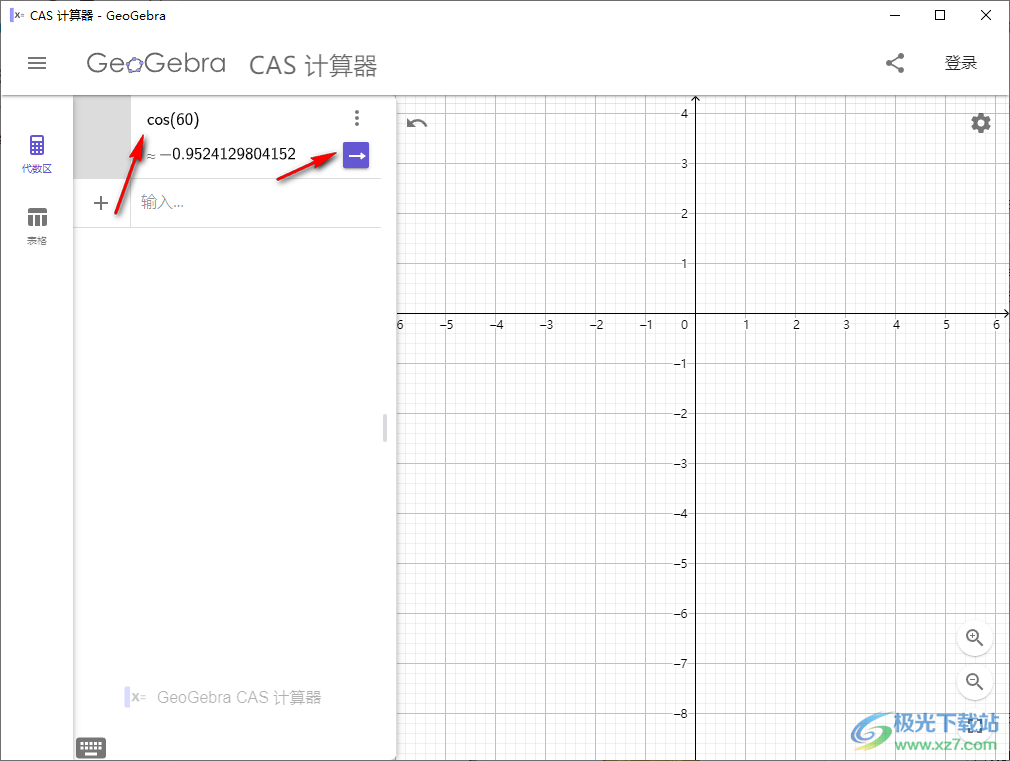
　　4、函数公式可以在绘图区域显示，输入一个函数表达式就可以在右侧的绘图界面显示

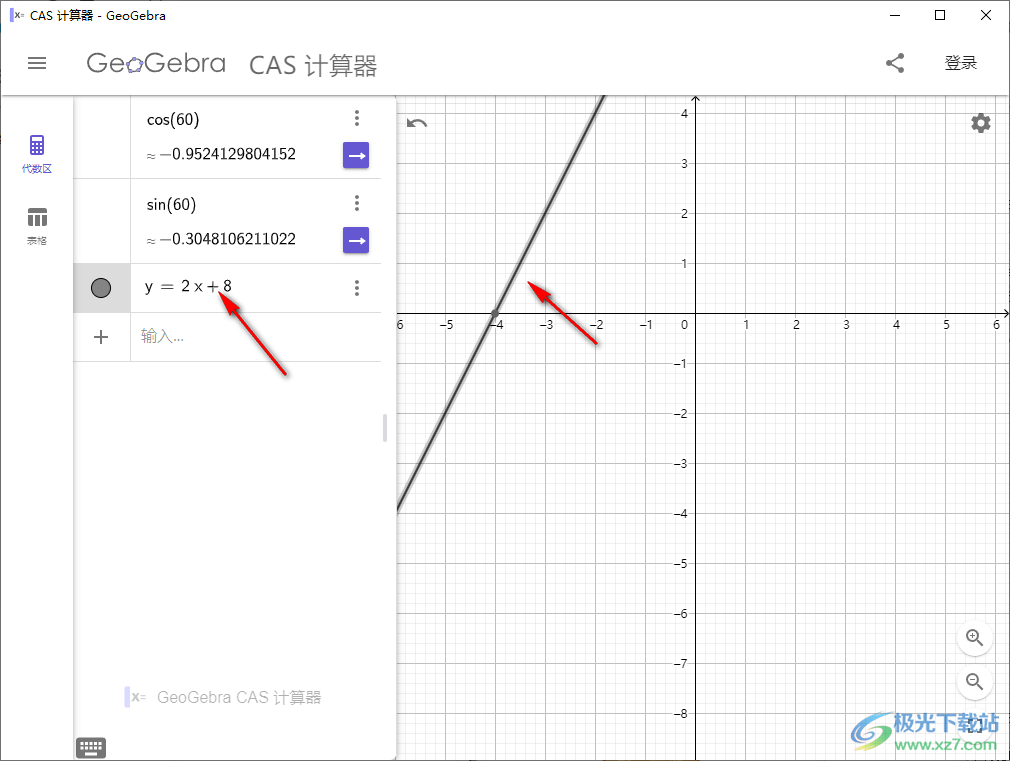
　　5、如果你需要在电脑上计算函数就可以选择GeoGebra CAS计算器，数学上常见的函数都可以通过这款软件分析

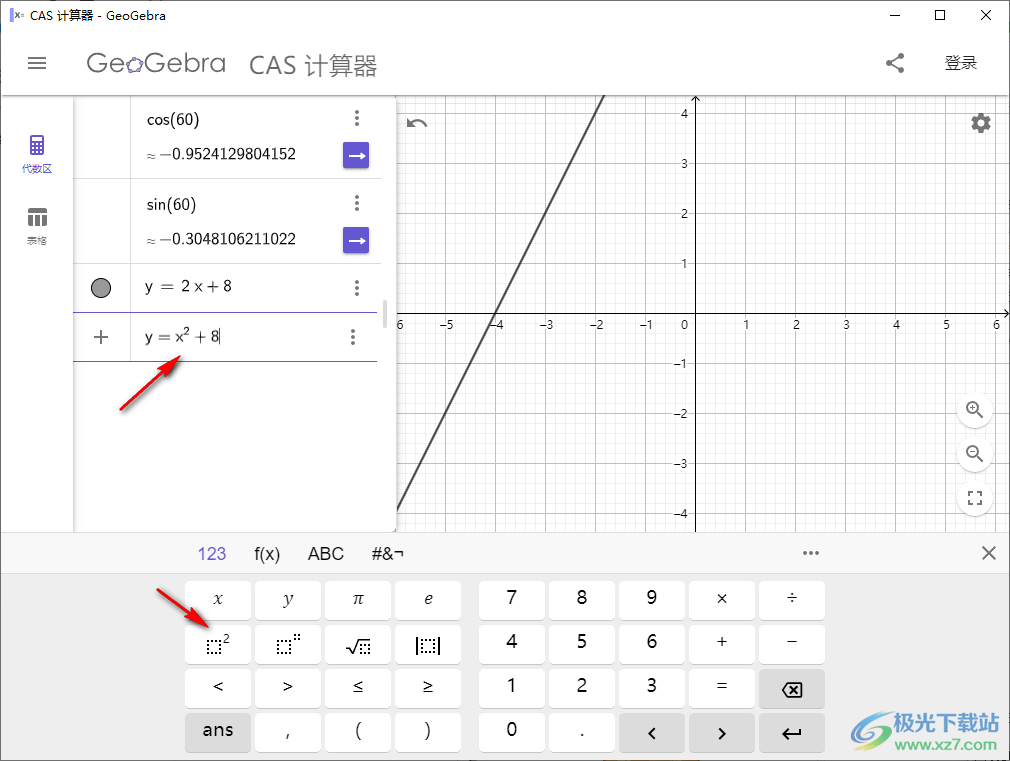
　　6、支持精确解、数值表、特殊点、添加标签、重复输入、删除、设置

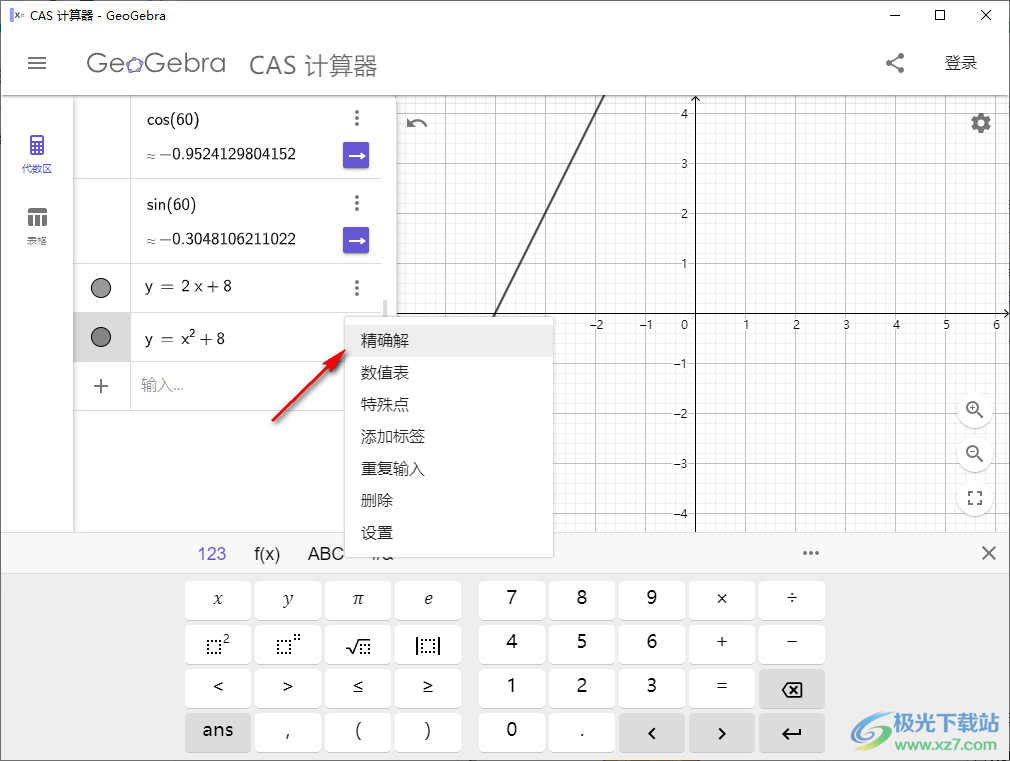
　　7、进入设置界面，可以定义函数内容，可以设置标签，可以便用文本作为标题、显示对象、显示标签：名称、辅助对象

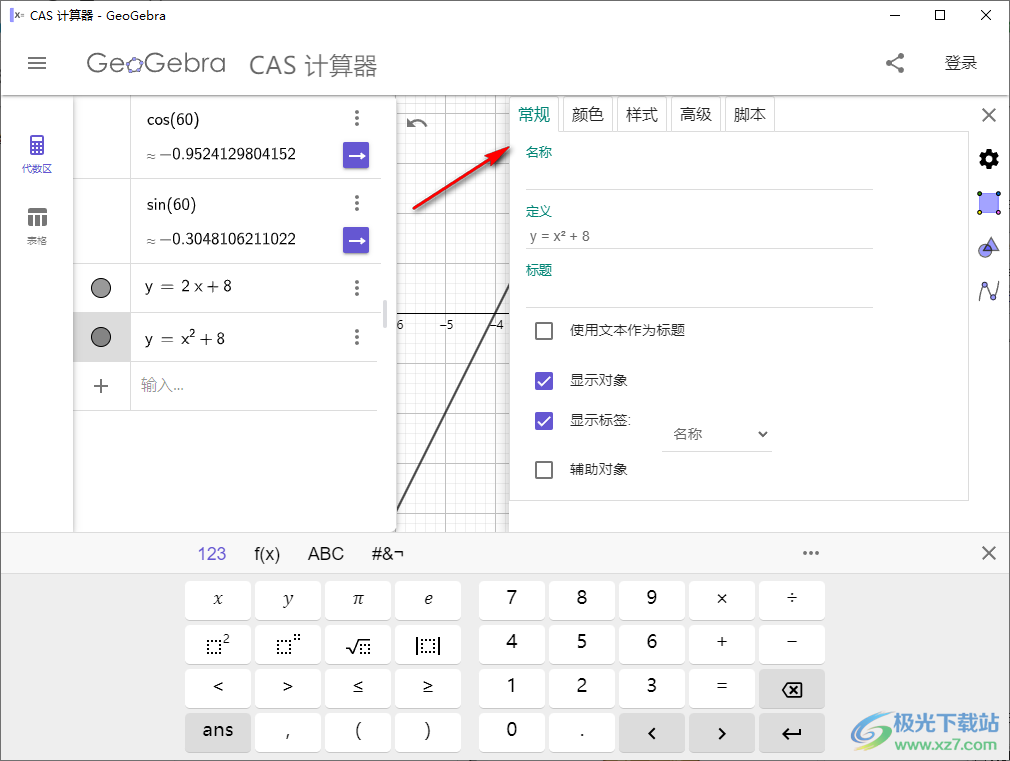
　　8、颜色设置界面，可以为你的表达式设置颜色，绘图界面也会显示函数的颜色

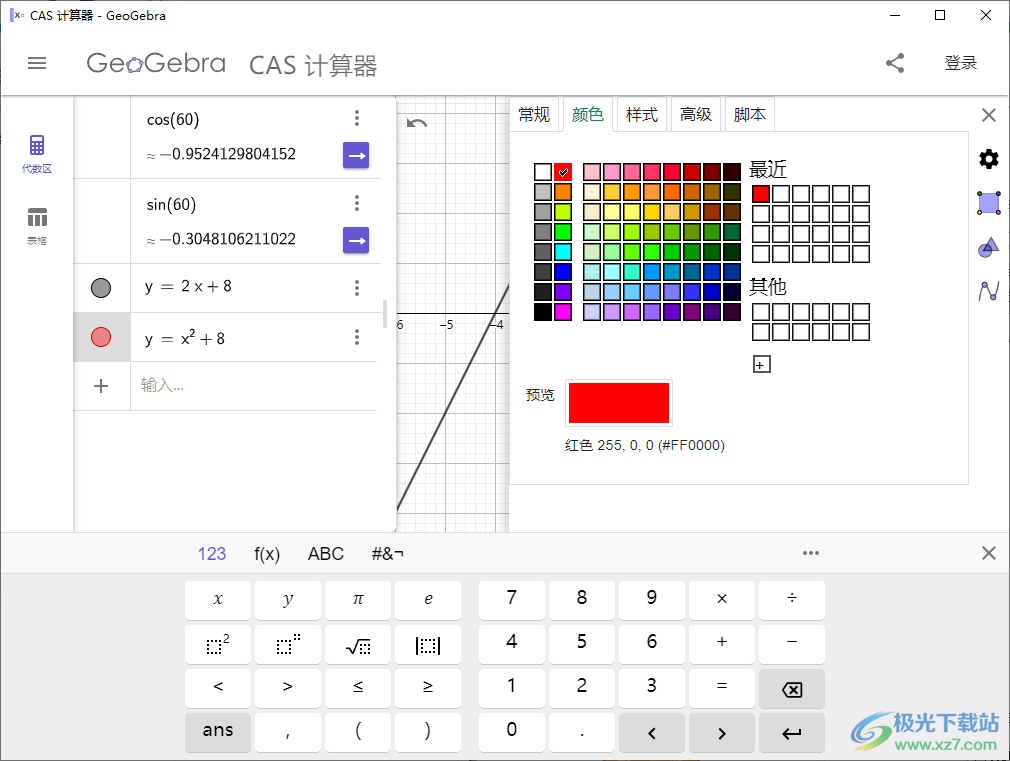
　　9、支持表格设置，可以通过表格输入数值，从而计算函数内容

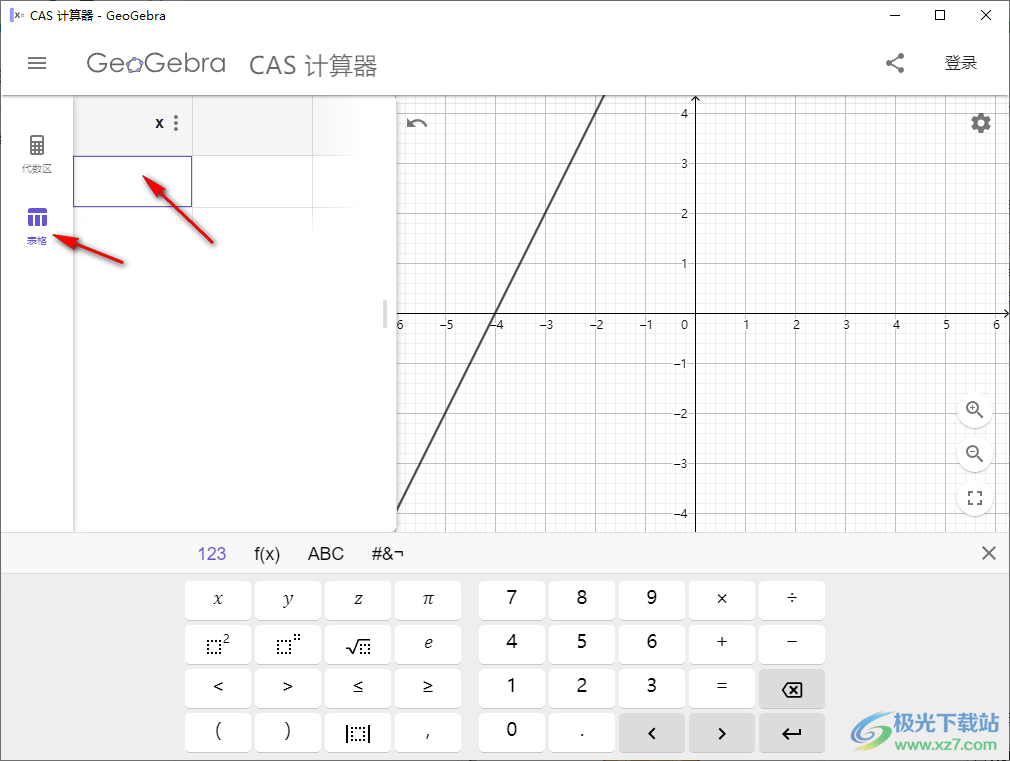
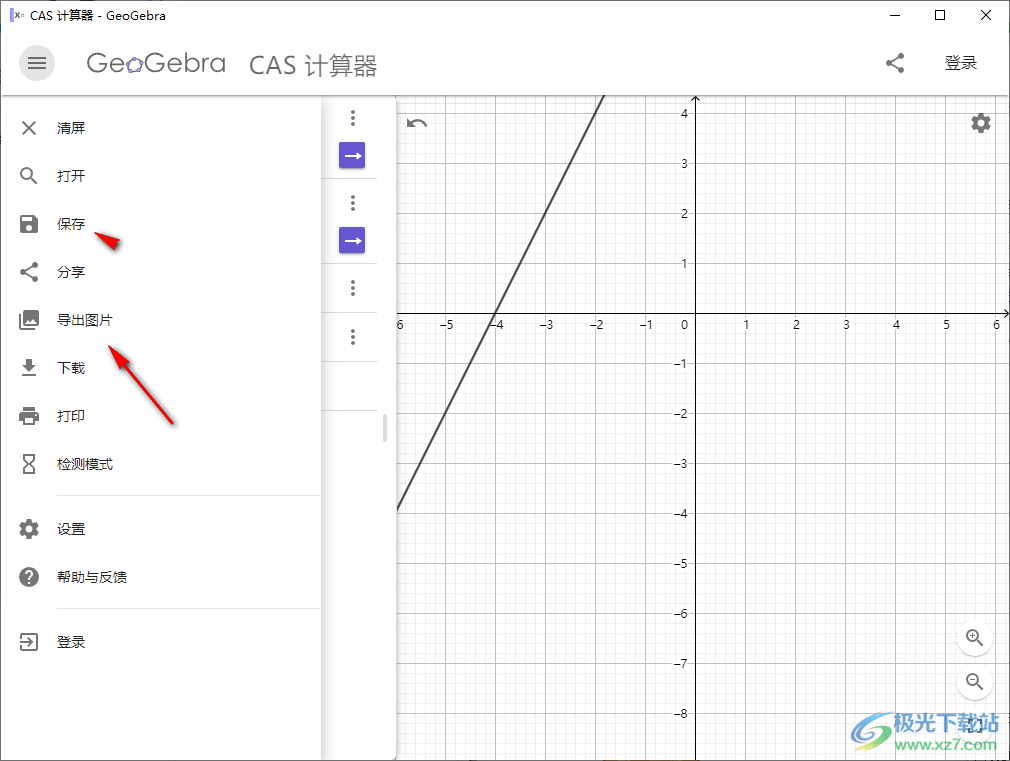
　　10、最后就是保存制作的内容，可以直接在软件保存，也可以在软件导出图像内容

官方教程

　　运算区输入的提示和技巧

　　引用其他行

　　静态行引用将复制输出, 但是随后更改了被引用行后, 它并不更新:

　　输入 #, 静态引用前一行的输出.

　　输入 #5, 静态引用第 5 行的输出.

　　动态行引用插入的是对其他行的引用, 而不是实际的输出, 因此, 如果随后更改了被引用行, 则它也将跟着更新:

　　输入 $ , 动态引用前一行的输出.

　　输入 $3 , 动态引用第 3 行的输出.

　　任务

　　请按照下面的指导, 对其他行进行引用.

　　指导

　　在第二行输入 a²-2*a*b.

　　在第三行计算 #1-$2 .

　　将第一行的输入更改为 (a-b)², 验证第三行的输出是否更改.

　　将第二行的输入更改为b²-2*a*b, 验证第三行的输出是否更.

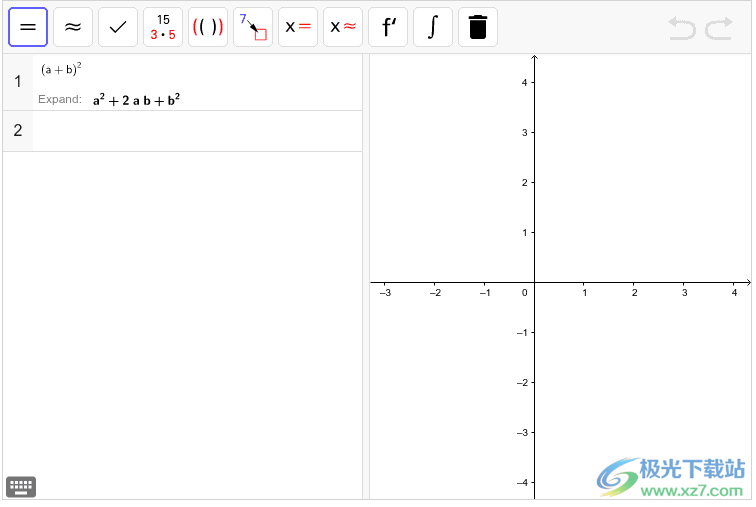
　　替换指令语法中的参数

　　从建议的指令列表中选择一个指令后, 第一个参数将自动突出显示, 并且可以轻松地用佻的输入进行代替. 要突出显示下一个参数, 请键入逗号或按 tab 键.

　　解方程组

　　任务

　　求鞍点为 (1, 1) 和 (2, 2) 的三次多项式函数.

　　指导

　　1. 在指令栏, 定义函数 f(x):= a x^3 + b x^2 + c x + d.

　　2. p 根据任务, 函数在 x=1 时的值是 1. 输入 p: f(1) = 1; , 然后按 Enter 键. 窍门: 冒号 ":" 是定义方程式, 而分号 “;” 是阻止输出.

　　3. q 我们也知道函数在 x=2 时的值是 2. 在指令栏输入 q: f(2) = 2;

　　4.r 因为 (1, 1) 是一个鞍点, 所以在 x=1 处的一阶导数等于 0. 输入 r: f'(1) = 0; 窍门: f 的导数可写为 f'.

　　5.s 我们也知道, 在 x=1 处的二阶导数等于 0. 输入 s: f''(1) = 0;

　　6.用指针选择第二到第五行, 然后应用精确解工具.

　　窍门:

　　在相应的行号上单击时, 按住 Ctrl-键以同时选择若干行.

　　您也可以使用精确解指令来实现相同的目的: Solve({p, q, r, s}, {a, b, c, d})

　　7.Substitute 在指令栏输入 Substitute($1, $6), 然后按 Enter 键. 注意: 您这是用刚计算出来的解集 ($6) 替换公式 f ($1) 中未定义的变量.

　　8. 激活行号 7 中禁用的可见性按钮, 在 绘图区绘制函数.